Обчислення визначників другого - четвертого порядку
Навчитися обчислювати визначники, обернені матриці і т.д. – одне з основних завдань для першокурсників, які здобувають освіту на факультетах з математичним нахилом в навчанні. Багато сервісів в інтернеті пропонують онлайн знаходження визначників і всього іншого, що стосується матриць, проте мало програм – математичних калькуляторів, які показують хід розв'язування. В кінці статті Вашій увазі пропонується такий калькулятор, але про це пізніше, а зараз давайте розглянемо декілька прикладів на знаходження визначника матриці.
За довідник візьмемо збірник задач Дубовика В.П., Юрика І.І. "Вища математика ". Пізніше будуть додані приклади обчислення визначника матриці з інших джерел.
Приклади. Обчислити визачник матриці
1) (1.4)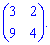
Застосуємо правило обчислення визначника для матриці другого порядку.
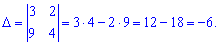
1) (1.4)
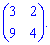
Застосуємо правило обчислення визначника для матриці другого порядку.
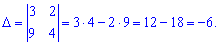
2) (1.6) 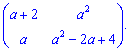
Знаходимо визначник другого порядку перехресним множенням
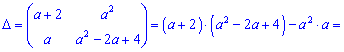
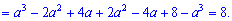
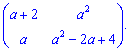
Знаходимо визначник другого порядку перехресним множенням
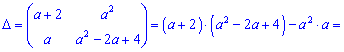
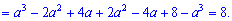
3) (1.8) 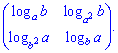
Даний приклад виглядає складним, бо містить логарифми, проте зі знанням наступних правил
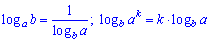
розв'язується напрочуд швидко.
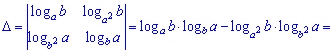
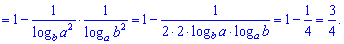
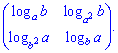
Даний приклад виглядає складним, бо містить логарифми, проте зі знанням наступних правил
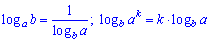
розв'язується напрочуд швидко.
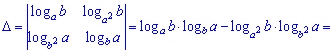
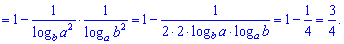
4) (1.14)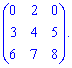
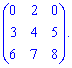
Обчислимо даний визначник двома способами: правилом трикутників та через алгебраїчні доповнення.
За формулою трикутників отримаємо
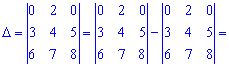
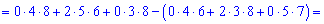
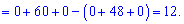
А зараз розкладемо за елементами першого рядка, оскільки в ньому найбільше нулів
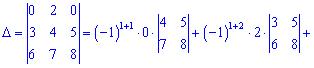
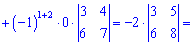
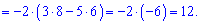
В цьому прикладі спеціально виписані доповнення біля нульових множників, оскільки не всі розуміють звідки беруться доповнення. За правилом вони рівні визначнику, який утворюється викреслюванням рядка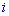 та стовпця
та стовпця 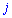 того елемента
того елемента 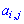 , для якого шукаються, помноженому на мінус одиницю в степені суми індексів
, для якого шукаються, помноженому на мінус одиницю в степені суми індексів 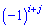 .
.
Схематично на прикладі матриці четвертого порядку це виглядає так:
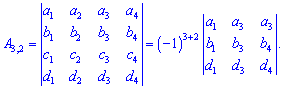
Уважно подивіться, які елементи у визначнику виписані для доповнень і Вам все стане зрозуміло.
За формулою трикутників отримаємо
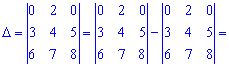
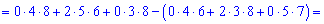
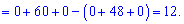
А зараз розкладемо за елементами першого рядка, оскільки в ньому найбільше нулів
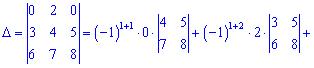
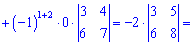
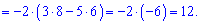
В цьому прикладі спеціально виписані доповнення біля нульових множників, оскільки не всі розуміють звідки беруться доповнення. За правилом вони рівні визначнику, який утворюється викреслюванням рядка
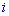 та стовпця
та стовпця 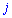 того елемента
того елемента 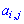 , для якого шукаються, помноженому на мінус одиницю в степені суми індексів
, для якого шукаються, помноженому на мінус одиницю в степені суми індексів 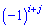 .
.Схематично на прикладі матриці четвертого порядку це виглядає так:
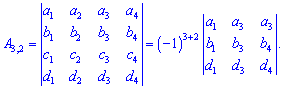
Уважно подивіться, які елементи у визначнику виписані для доповнень і Вам все стане зрозуміло.
Суть методу алгебраїчних доповнень полягає в тому, що коли ми маємо матрицю з нульовими елементами то, розклавши її за за рядком чи стовпцем в якому найбільше нулів нам залишається обчислити стільки визначників на порядок менших від основної матриці, скільки є ненульових елементів. Це значно спрощує обчислення.
6) (1.19) 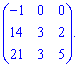
Якщо обчислення проводити за правилом трикутників, то отримаємо багато нульових добутків. В такого роду прикладах доцільно використовувати алгебраїчні доповнення.
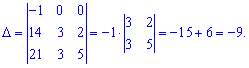
Ось для чого і потрібно використовувати властивості визначників - для спрощення обчислень.
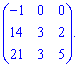
Якщо обчислення проводити за правилом трикутників, то отримаємо багато нульових добутків. В такого роду прикладах доцільно використовувати алгебраїчні доповнення.
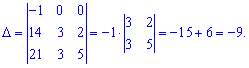
Ось для чого і потрібно використовувати властивості визначників - для спрощення обчислень.
7) (1.21) 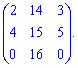
Обчислимо визначник через алгебраїчні доповнення третього рядка. Він вигідний тим, що містить два нульові елементи матриці
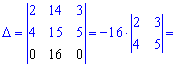
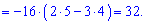
Як можна переконатися, розв'язок з допомогою алгебраїчних доповнень у випадках розріджених матриць можна отримати швидко і без великої кількості обчислень.
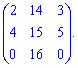
Обчислимо визначник через алгебраїчні доповнення третього рядка. Він вигідний тим, що містить два нульові елементи матриці
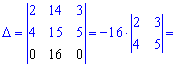
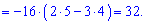
Як можна переконатися, розв'язок з допомогою алгебраїчних доповнень у випадках розріджених матриць можна отримати швидко і без великої кількості обчислень.
8) (1.58) 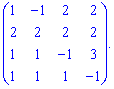
Виконаємо елементарні перетворення - від другого рядка віднімемо перший, а від четвертого – третій. Отримаємо розріджену матрицю
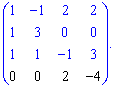
При цьому знак не помняється, бо ми не змінювали рядки місцями. Визначник знайдемо через алгебраїчні доповнення до четвертого рядка
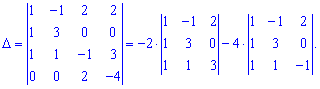
Обчислимо кожен з доданків
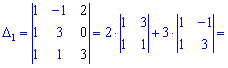
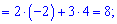
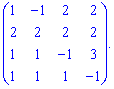
Виконаємо елементарні перетворення - від другого рядка віднімемо перший, а від четвертого – третій. Отримаємо розріджену матрицю
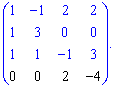
При цьому знак не помняється, бо ми не змінювали рядки місцями. Визначник знайдемо через алгебраїчні доповнення до четвертого рядка
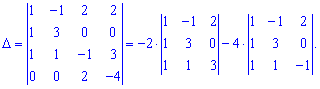
Обчислимо кожен з доданків
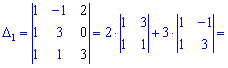
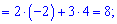
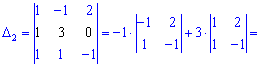
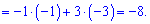
Підставляємо у визначник та сумуємо
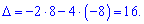
Ось так швидко порахували детермінант 4 порядку.
9) (1.72) 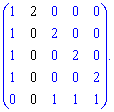
Знайдемо визначник через розклад за рядками і стовпцями, що містять нулі (виділені чорним).
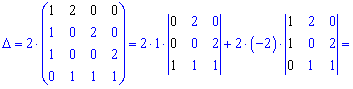
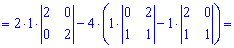
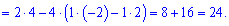
Таким методом знаходження визначника п'ятого порядку звелося до простих обчислень. Практикуйте та вчіть правила і через деякий час у Вас виходитиме не гірше. До зустрічі в наступних уроках!

Знайдемо визначник через розклад за рядками і стовпцями, що містять нулі (виділені чорним).
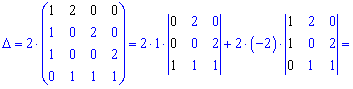
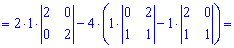
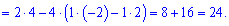
Таким методом знаходження визначника п'ятого порядку звелося до простих обчислень. Практикуйте та вчіть правила і через деякий час у Вас виходитиме не гірше. До зустрічі в наступних уроках!
Немає коментарів:
Дописати коментар