Визначник 4 порядку.
Визначники четвертого та старших порядків можливо обчислювати за спрощеними схемами, які полягають в розкладі за елементами рядків або стовпців та зведенні до трикутного вигляду. Обидва методи для наочності будуть розглянуті на матрицях 4-го порядку.
Метод розкладу за елементами рядків або стовпців
Перший приклад ми розглянемо з детальними поясненнями усіх проміжних дій.
Приклад 1. Обчислити визначник матриці 4х4 методом розкладу.


Розв'язання. Для спрощення обчислень розкладемо визначник четвертого порядку за елементами першого рядка (містить нульовий елемент). Вони утворюються множенням елементів на відповідні їм доповнення (утворюються викреслення рядків та стовпців на перетині елемента, для якого обчислюються - виділено червоним)
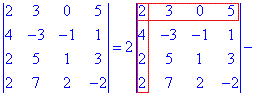
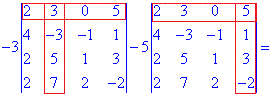
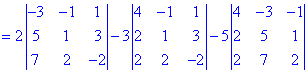
В результаті обчислення зведуться до відшукання трьох визначників третього порядку. Їх знаходимо за правилом трикутників
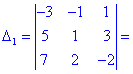
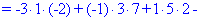
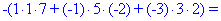
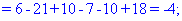
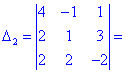
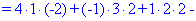
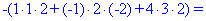
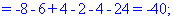
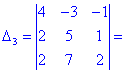
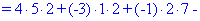
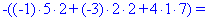
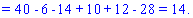
Знайдені значення підставляємо в вихідний детермінант
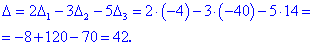


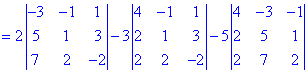
В результаті обчислення зведуться до відшукання трьох визначників третього порядку. Їх знаходимо за правилом трикутників
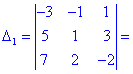
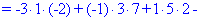
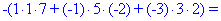
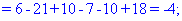
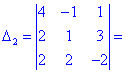
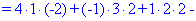
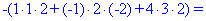
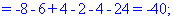
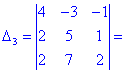
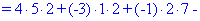
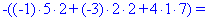
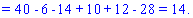
Знайдені значення підставляємо в вихідний детермінант
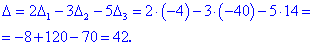
Результат легко перевіріті с помощью матричного калькулятора YukhymCALC . Для цього вібіраємо пункт матриці-Візначнік матриці, розмір матриці що вводяться 4 * 4.
Записуємо саму матрицю та здійснюємо обчислення. Результатом розрахунків буде наступний вивід даних
 Результати співпадають, отже обчислення проведені вірно.
Результати співпадають, отже обчислення проведені вірно.
Приклад 2. Обчислити визначник матриці четвертого порядку.

Розв'язання. Як і в попередньому завданні виконуємо обчислення методом розкладу. Для цього виберемо елементи першого стовпця. Спрощено визначник матриці 4х4 можна подати через суму чотирьох детермінантів третього порядку у вигляді
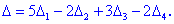
Далі переходимо до відшукання визначників за правилом трикутників
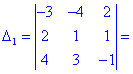
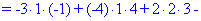
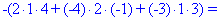
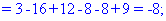
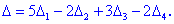
Далі переходимо до відшукання визначників за правилом трикутників
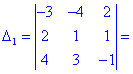
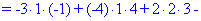
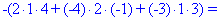
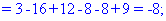
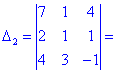
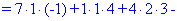
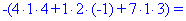
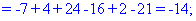
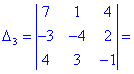
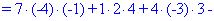
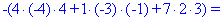
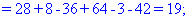
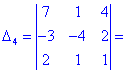
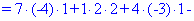
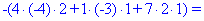
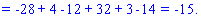
Обчислення не надто складні, головне не напутати зі знаками та при виборі трикутників. Знайдені величини підставляємо в головний визначник матриці та підсумовуємо
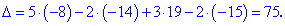
Результат перевіряємо матричним калькулятором YukhymCALC . Правильність розрахунків підтверджується наступним малюнком

Метод зведення визначника до трикутного вигляду
Даний метод дозволяє ряд визначників обчислити в досить швидкий спосіб. Суть його полягає у зведенні визначника до трикутного вигляду, при цьому слід враховувати всі множники на які збільшуємо чи зменшуємо рядки та врахуванні при кінцевих розрахунках. З даного визначення Ви нічого для себе не зрозумієте, тому краще все показати на конкретних прикладах.
Приклад 3. Знайти визначник матриці зведенням до трикутного вигляду
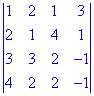
Розв'язання. Спочатку здійснюємо математичні маніпуляції, щоб отримати всі нульові елементи окрім першого в першому стовпці. Для цього від другого рядка віднімаємо перший, помножений на два. В результаті отримаємо
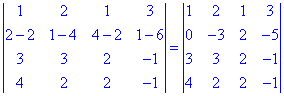
Далі є два варіанти: від третього рядка відняти перший помножений на три, або від третього відняти суму перших двох рядків. Останній варіант дозволить отримати зразу два нулі в рядку, його і вибираємо
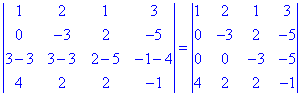
Дальше доцільніше від четвертого відняти подвоєний другий рядок. В результаті елементарних перетворень визначник набуде вигляду
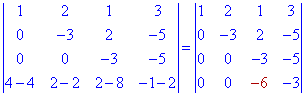
Залишилося перетворити в нуль один елемент в третьому стовпці. Для цього від четвертого рядка віднімаємо подвоєний третій в попередньо записаному визначнику
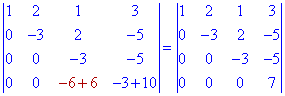
Визначник трикутної матриці рівний добутку діагональних елементів.
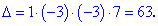
За бажанням можна первірити результат матричним калькулятором. В цьому прикладі ніяких домножень рядків, в яких занулювали елементи ми не виконували, то ж повністю розкрити метод на цьому прикладі не получилося. Розглянемо складніший.
В цьому прикладі ніяких домножень рядків, в яких занулювали елементи ми не виконували, то ж повністю розкрити метод на цьому прикладі не получилося. Розглянемо складніший.
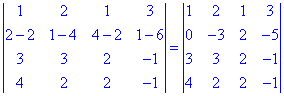
Далі є два варіанти: від третього рядка відняти перший помножений на три, або від третього відняти суму перших двох рядків. Останній варіант дозволить отримати зразу два нулі в рядку, його і вибираємо
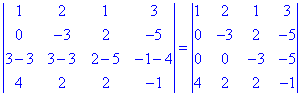
Дальше доцільніше від четвертого відняти подвоєний другий рядок. В результаті елементарних перетворень визначник набуде вигляду
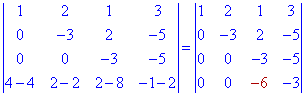
Залишилося перетворити в нуль один елемент в третьому стовпці. Для цього від четвертого рядка віднімаємо подвоєний третій в попередньо записаному визначнику
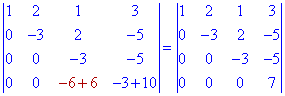
Визначник трикутної матриці рівний добутку діагональних елементів.
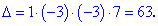
За бажанням можна первірити результат матричним калькулятором.
 В цьому прикладі ніяких домножень рядків, в яких занулювали елементи ми не виконували, то ж повністю розкрити метод на цьому прикладі не получилося. Розглянемо складніший.
В цьому прикладі ніяких домножень рядків, в яких занулювали елементи ми не виконували, то ж повністю розкрити метод на цьому прикладі не получилося. Розглянемо складніший.
Приклад 4. Знайти визначник матриці 4-го порядку
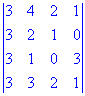 Розв'язання. Елементарними перетвореннями зводимо визначник до трикутного вигляду. Для цього від кожного рядка віднімаємо перший. В результаті перетворень отримаємо наступний детермінант
Розв'язання. Елементарними перетвореннями зводимо визначник до трикутного вигляду. Для цього від кожного рядка віднімаємо перший. В результаті перетворень отримаємо наступний детермінант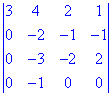
Для зручності обчислень, міняємо третій рядок з другим місцями.

За властивістю визначників, будь-яка заміна рядків місцями веде до зміни знаку визначника. Враховуємо це у деякому множнику k=-1.
Від третього рядка віднімаємо другий, помножений на мінус три. Після спрощень отримаємо

Перетворюємо в нуль останній елемент в другому стовпці, для цього віднімаємо другий рядок помножений на 2. Результат буде наступним

Від подвоєного четвертого рядка віднімаємо третій. За властивістю, домноження рядка на сталу а веде до зміни визначника в а раз. Дану зміну фіксуємо в множнику k=-1*2=-2.

Остаточне значення визначника буде рівне добутку діагональних елементів поділених (або нормованих) на множник k,який відповідає за зміну детермінанта при елементарних перетвореннях. Виконуємо обчислення
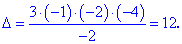
Перевірка матричним калькулятором підтверджує правильність здійснених обчислень.
 Метод розкладу визначника за елементами рядків чи стовпців доцільно застосоввати при знаходженні детермінантів матриць 4х4 та більих розмірів. Метод зведення до трикутного вигляду ефективний, якщо елементарні перетворення легко прослідкувати і не призводять до великих добутків. В інших випадках потрібно користуватися комбінацією цих методів, останнім утворювати якомога більше нульових елементів, а методом розкладу за рядками чи стовпцями зменшувати кількість виконаних операцій. Це дозволить без проблем обчислювати визначники третього, четвертого і навіть п'ятого порядку.
Метод розкладу визначника за елементами рядків чи стовпців доцільно застосоввати при знаходженні детермінантів матриць 4х4 та більих розмірів. Метод зведення до трикутного вигляду ефективний, якщо елементарні перетворення легко прослідкувати і не призводять до великих добутків. В інших випадках потрібно користуватися комбінацією цих методів, останнім утворювати якомога більше нульових елементів, а методом розкладу за рядками чи стовпцями зменшувати кількість виконаних операцій. Це дозволить без проблем обчислювати визначники третього, четвертого і навіть п'ятого порядку.
Немає коментарів:
Дописати коментар