Визначник матриці 3x3
Знайти визначник матриці 3*3 можна швидко за правилом трикутника
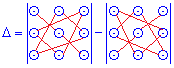Визначники позначають наступними знаками det(A), |A|, delta
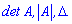Далі наведені приклади обчислення визначників.
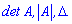Визначники позначають наступними знаками det(A), |A|, deltaДалі наведені приклади обчислення визначників.
Приклад 1. Знайти визначник матриці
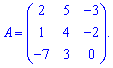Розв'язання: Застосовуємо правило трикутника для знаходження визначника
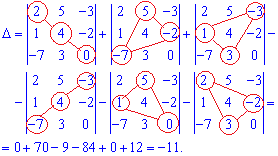
Визначник рівний 11.
Наведена схема стане Вам в нагоді для обчислення визначника матриці 3*3. Все що Вам потрібно – підставити свої значення
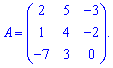Розв'язання: Застосовуємо правило трикутника для знаходження визначникаВизначник рівний 11.
Наведена схема стане Вам в нагоді для обчислення визначника матриці 3*3. Все що Вам потрібно – підставити свої значення
Приклад 2. Обчислити визначник матриці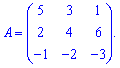
Розв'язання: З метою навчити Вас чогось нового, знайдемо визначник матриці за правилом Саррюса.
Схема обчислень приведена вище, тому копіювати її не будемо, а лише розпишемо в деталях. Для цього дописуємо до стандартного визначника два перші стовпці і виконуємо наступні розрахунки .
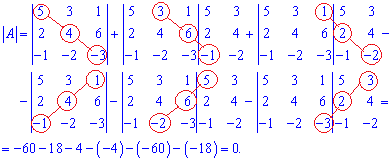
Обчислення не сладні, і тут допустити помилку набагато складніше ніж в правилі трикутника. Там Ви можете помилитися з розміщенням трикутника, зі знаком, а в правилі Саррюса все набагато спрощено.
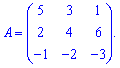Розв'язання: З метою навчити Вас чогось нового, знайдемо визначник матриці за правилом Саррюса.Схема обчислень приведена вище, тому копіювати її не будемо, а лише розпишемо в деталях. Для цього дописуємо до стандартного визначника два перші стовпці і виконуємо наступні розрахунки .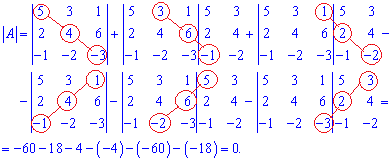Обчислення не сладні, і тут допустити помилку набагато складніше ніж в правилі трикутника. Там Ви можете помилитися з розміщенням трикутника, зі знаком, а в правилі Саррюса все набагато спрощено.
Приклад 3. Знайти визначник матриці 3*3
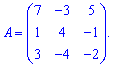Розв'язання: Застосовуємо правило трикутника для знаходження визначника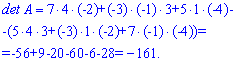
Детермінант рівний -161.
Приклад 4. Обчислити визначник матриці
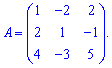Розв'язання: Знаходимо визначник матриці 3*3 за правилом трикутників
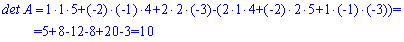
В результаті отримаємо десятку.
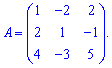Розв'язання: Знаходимо визначник матриці 3*3 за правилом трикутників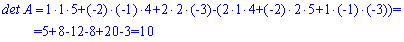В результаті отримаємо десятку.
Приклад 5. Знайти визначник матриці
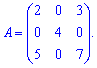Розв'язання: Матриця має декілька нульових елементів. Такі матриці ще називають розрідженими. Для зменшення кількості операцій обчислимо визначник через алгебраїчні доповнення до другого рядка або стовпця .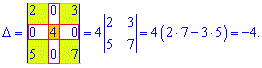
Простіше вже не може бути. Це набагато зручніше, ніж виписувати 6 добутків, чотири з ких дадуть нуль.
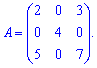Розв'язання: Матриця має декілька нульових елементів. Такі матриці ще називають розрідженими. Для зменшення кількості операцій обчислимо визначник через алгебраїчні доповнення до другого рядка або стовпця .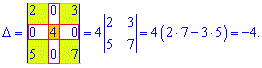Простіше вже не може бути. Це набагато зручніше, ніж виписувати 6 добутків, чотири з ких дадуть нуль.
Приклад 6. Довести, що визначник матриці А рівний 3.
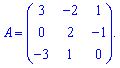Розв'язання: Матриця містить два нульових елементи, тому можемо знайти визначник через алгебраїчні доповнення. Розкладемо визначник за елементами першого стовпця.
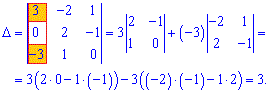
Визначник рівний 3, що і треба було доказати.
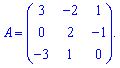Розв'язання: Матриця містить два нульових елементи, тому можемо знайти визначник через алгебраїчні доповнення. Розкладемо визначник за елементами першого стовпця.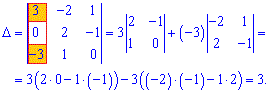Визначник рівний 3, що і треба було доказати.
Приклад 7. Знайти визначник матриці
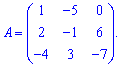Розв'язання: Детермінант матриці обчислюємо через алгебраїчні доповнення першого рядка або третього стовпця. Виконуємо розрахунки
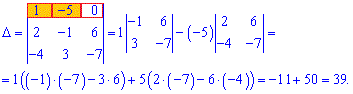
Визначник рівний 39.
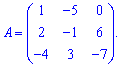Розв'язання: Детермінант матриці обчислюємо через алгебраїчні доповнення першого рядка або третього стовпця. Виконуємо розрахунки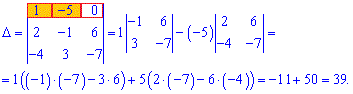Визначник рівний 39.
Приклад 8. При яких значеннях параметра а визначник матриці рівний нулеві
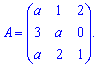Розв'язання: Завдання з параметром - це вже новий рівень обчислень, тому вивчайте схему.За правилом трикутників знаходимо визначник
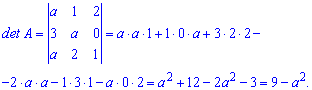
За умовою прирівнюємо визначник до нуля та знаходимо параметр
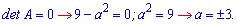
Є два параметри при яких визначник перетворюється в нуль a=-3;a=3.
Приклад 9. Знайти визначник матриці
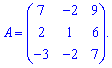Розв'язання: Обчислимо визначник матриці за правилом трикутників та через алгебраїчні доповнення. За першою схемою отримаємо
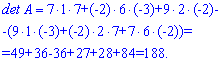
Тепер розкладемо за допомогою алгебраїчних доповнень, наприклад, за третім стовпцем. Він зручний тим, що містить найбільші елементи матриці. Знаходимо визначник
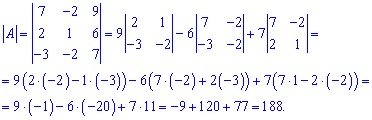
Порівнянням кількості розрахунків переконуємося, що в таких випадках доцільніше використовувати правило трикутників. Обчислення простіші і менша ймовірність зробити помилку.
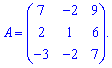Розв'язання: Обчислимо визначник матриці за правилом трикутників та через алгебраїчні доповнення. За першою схемою отримаємо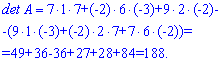Тепер розкладемо за допомогою алгебраїчних доповнень, наприклад, за третім стовпцем. Він зручний тим, що містить найбільші елементи матриці. Знаходимо визначник
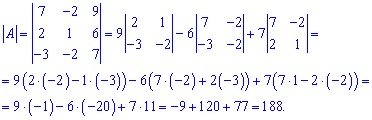
Порівнянням кількості розрахунків переконуємося, що в таких випадках доцільніше використовувати правило трикутників. Обчислення простіші і менша ймовірність зробити помилку.
Для розріджених матриць чи більшого порядку блочних вартує застосовувати розклад визначника за рядком чи стовпцем.
І наостанок бонус від нас – матричний калькулятор YukhymCalc.
І наостанок бонус від нас – матричний калькулятор YukhymCalc.
З його допомогою Ви легко перевірите правильність виконання основних операцій з матрицями, а також зможете знайти визначник матриці та обернену матрицю. Для матриць 3*3 використовується правило трикутників, для 4*4 – розклад визначника через елементи першого рядка. Меню досить просте та інтуїтивно зрозуміле не ті.Визначник 7 завдання через матричний калькулятор матиме наступний виглядьки студенту, а й школяру.
Перевага матричного калькулятора перед іншими, зокрема онлайн –калькуляторами, в тому, що Ви бачите всі проміжні операції. А це важливо для перевірки та контролю помилок.
Використовуйте наведені схеми обчислень визначників у навчанні. Якщо виникають труднощі в обчисленнях та є можливість, то можете перевірити знайдені визначники калькулятором. Завантажити матричний калькулятор YukhymCalc Ви можете без реєстрації за цим посиланням.
Немає коментарів:
Дописати коментар