Знаходження добутку матриць
Добутком двох матриць буде матриця A, елементи якої Ai,j рівні сумі попарних добутків елементів рядка першої матриці B на відповідні елементи стовпця другої матриці C: 
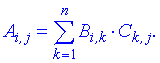 З цього слідує, що перемножити між собою можна матриці в яких кількість стовпців першої B рівна кількості рядків другої C. Нова матриця A, яка є добутком двох, має розмірність m*n, де m – кількість рядків першої матриці, а n – стовпців другої. Правила досить прості, і для знаходження добутку матриць потрібно вміти множити і додавати. Розглянемо кілька прикладів зі збірника задач Дубовика В.П., Юрика І.І. "Вища математика".
З цього слідує, що перемножити між собою можна матриці в яких кількість стовпців першої B рівна кількості рядків другої C. Нова матриця A, яка є добутком двох, має розмірність m*n, де m – кількість рядків першої матриці, а n – стовпців другої. Правила досить прості, і для знаходження добутку матриць потрібно вміти множити і додавати. Розглянемо кілька прикладів зі збірника задач Дубовика В.П., Юрика І.І. "Вища математика".

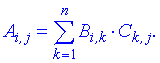 З цього слідує, що перемножити між собою можна матриці в яких кількість стовпців першої B рівна кількості рядків другої C. Нова матриця A, яка є добутком двох, має розмірність m*n, де m – кількість рядків першої матриці, а n – стовпців другої. Правила досить прості, і для знаходження добутку матриць потрібно вміти множити і додавати. Розглянемо кілька прикладів зі збірника задач Дубовика В.П., Юрика І.І. "Вища математика".
З цього слідує, що перемножити між собою можна матриці в яких кількість стовпців першої B рівна кількості рядків другої C. Нова матриця A, яка є добутком двох, має розмірність m*n, де m – кількість рядків першої матриці, а n – стовпців другої. Правила досить прості, і для знаходження добутку матриць потрібно вміти множити і додавати. Розглянемо кілька прикладів зі збірника задач Дубовика В.П., Юрика І.І. "Вища математика".
Приклади. Знайти добуток матриць.
1) (1.110) 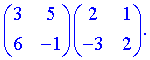
Для знаходження добутку перемножуємо рядки першої матриці на стовпці другої
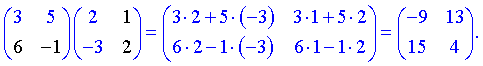
На цьому і побудована операція множення, необхідно почленно перемножити елементи рядка першої матриці на елементи стовпця другої матриці та просумувати. Звідси випливають і властивості добутку матриць, і обмеження на матриці (які можна перемножити, а які ні).
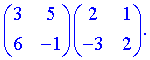
Для знаходження добутку перемножуємо рядки першої матриці на стовпці другої
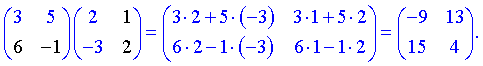
На цьому і побудована операція множення, необхідно почленно перемножити елементи рядка першої матриці на елементи стовпця другої матриці та просумувати. Звідси випливають і властивості добутку матриць, і обмеження на матриці (які можна перемножити, а які ні).
2) (1.112) 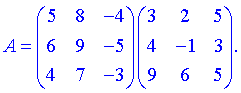
За формулою множення знайдемо елементи нової матриці
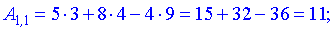
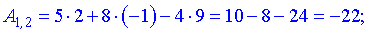
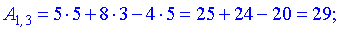
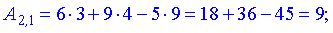
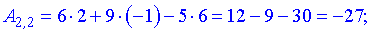
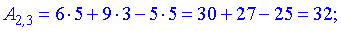
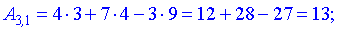
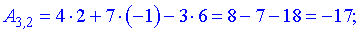
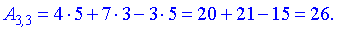
Записуємо отримані значення в матрицю.
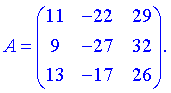
Це і є шуканий резуьтат добутку двох матриць.
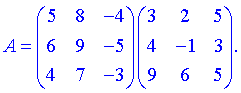
За формулою множення знайдемо елементи нової матриці
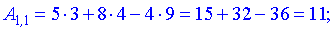
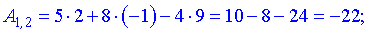
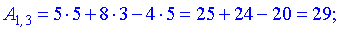
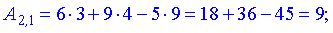
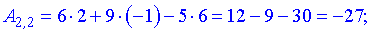
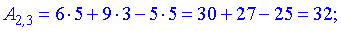
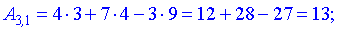
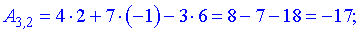
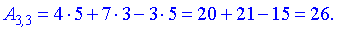
Записуємо отримані значення в матрицю.
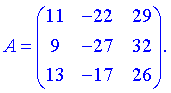
Це і є шуканий резуьтат добутку двох матриць.
3) (1.114) 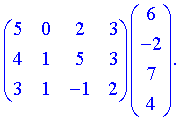
За правилами добутком буде матриця-вектор розмірності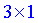 . Обчислимо її елементи
. Обчислимо її елементи
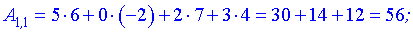
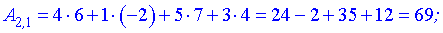
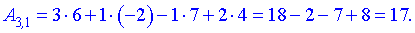
Остаточно матриця набуде вигляду
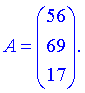
Хоча це біьше усім нагадує вектор, проте це матриця одиничної розмірності.
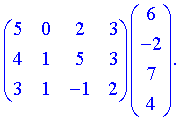
За правилами добутком буде матриця-вектор розмірності
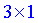 . Обчислимо її елементи
. Обчислимо її елементи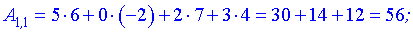
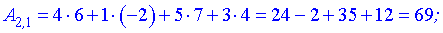
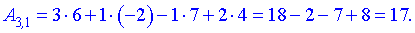
Остаточно матриця набуде вигляду
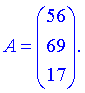
Хоча це біьше усім нагадує вектор, проте це матриця одиничної розмірності.
4) (1.115) 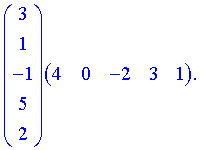
При обчисленні добутку матриць-векторів отримаємо квадратну матрицю розміру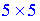 .
.
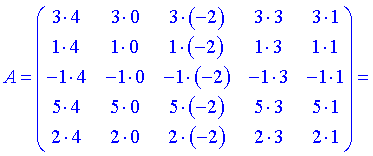
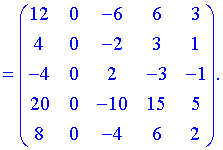
При цьому операцій мінімум, а отримана нова квадратна матриця має п'ятий порядок.
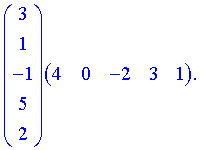
При обчисленні добутку матриць-векторів отримаємо квадратну матрицю розміру
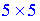 .
.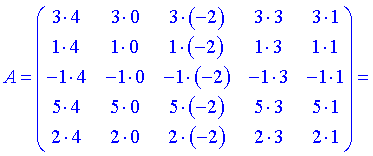
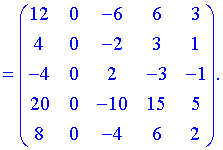
При цьому операцій мінімум, а отримана нова квадратна матриця має п'ятий порядок.
5) (1.116) 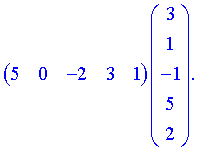
Результатом множення в даному прикладі буде матриця, яка містить лише один елемент.
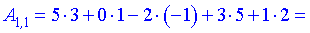
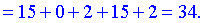
А все тому, що перша матриця має 1 рядок, а друга - один стовпець!
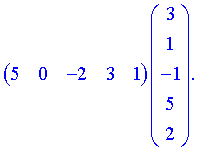
Результатом множення в даному прикладі буде матриця, яка містить лише один елемент.
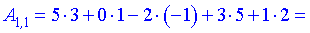
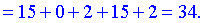
А все тому, що перша матриця має 1 рядок, а друга - один стовпець!
На цьому практична частина уроку завершена. Вправляйтесь в розв'язуванні подібних прикладів, адже множення - це одна з основних операцій (не тільки в матрицях). В наступних статтях матеріал буде складніший, тож починайте знайомитися з матрицями з простого.
Немає коментарів:
Дописати коментар