Обернена матриця 3*3.
Як знайти обернену матрицю детально описано в попередніх уроках. Нагадаю лише послідовність обчислень:
- знаходимо визначник головної матриці;
- далі через мінори обчислюємо алгебраїчні доповнення до матриці;
- останнім кроком потрібно протранспонувати матрицю алгебраїчних доповнень (знайти союзну) та поділити на визначник.
- Результатом обчислень і буде обернена матриця.
Нижче наведені приклади покрокового обчислення матриці 3х3. Інструкція дуже добре проілюстрована, тому Вам все стане зрозуміло з першого перегляду.
Приклад 1. Знайти обернену матрицю
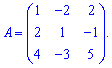
Розв'язання: Обчислюємо визначник матриці 3*3 за правилом трикутників
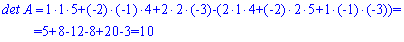
Визначник відмінний від нуля, отже матриця А не вироджена і існує обернена до неї.
Алгебраїчні доповнення рівні мінорам помноженим на (-1) в степені суми рядка і стовпця елемента матриці.
Для простоти можете використовувати наведену нижче схему знаків мінорів
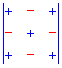 Мінори рівні визначникам на 1 меншого порядку ніж матриця, які утворюються викреслюванням рядка та стовпця на перетині якого знаходиться елемент. Більш зрозуміло стане з наступних прикладів обчислень алгебраїчних доповнень
Мінори рівні визначникам на 1 меншого порядку ніж матриця, які утворюються викреслюванням рядка та стовпця на перетині якого знаходиться елемент. Більш зрозуміло стане з наступних прикладів обчислень алгебраїчних доповнень
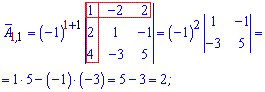
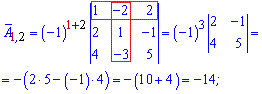
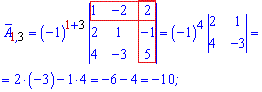
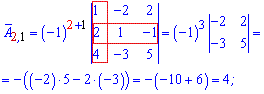
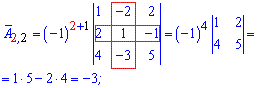
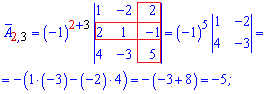
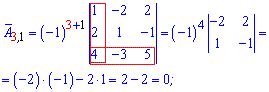
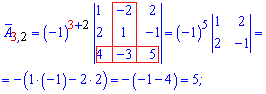
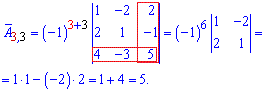
Із знайдених значень формуємо матрицю алгебраїчних доповнень
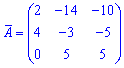
Транспонуємо її щоб отримати приєднану (союзну) матрицю
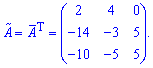
На цьому кроці будьте уважними – можна виконати правильно наведені вище обчислення і через невміння транспонувати отримати невірний результат.
Ділимо на визначник і отримуємо обернену матрицю
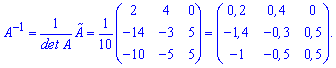
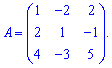
Розв'язання: Обчислюємо визначник матриці 3*3 за правилом трикутників
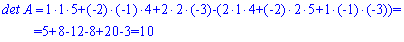
Визначник відмінний від нуля, отже матриця А не вироджена і існує обернена до неї.
Алгебраїчні доповнення рівні мінорам помноженим на (-1) в степені суми рядка і стовпця елемента матриці.
Для простоти можете використовувати наведену нижче схему знаків мінорів
 Мінори рівні визначникам на 1 меншого порядку ніж матриця, які утворюються викреслюванням рядка та стовпця на перетині якого знаходиться елемент. Більш зрозуміло стане з наступних прикладів обчислень алгебраїчних доповнень
Мінори рівні визначникам на 1 меншого порядку ніж матриця, які утворюються викреслюванням рядка та стовпця на перетині якого знаходиться елемент. Більш зрозуміло стане з наступних прикладів обчислень алгебраїчних доповнень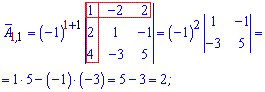
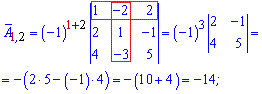
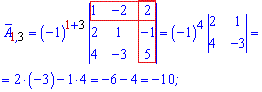
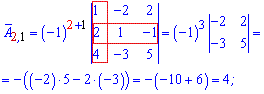

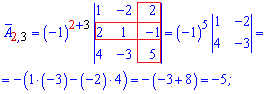
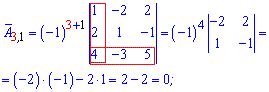
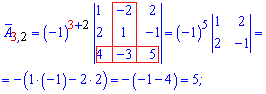
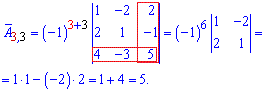
Із знайдених значень формуємо матрицю алгебраїчних доповнень
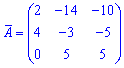
Транспонуємо її щоб отримати приєднану (союзну) матрицю
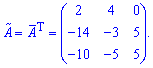
На цьому кроці будьте уважними – можна виконати правильно наведені вище обчислення і через невміння транспонувати отримати невірний результат.
Ділимо на визначник і отримуємо обернену матрицю
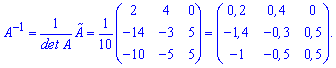
Знайти обернену мартицю Вам допоможе калькулятор оберненої матриці YukhymCalc. Для цього заходите в меню калькулятора і вибираєте обчислення обернених матриць
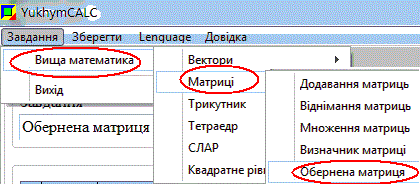 Далі задаєте розмір матриці
Далі задаєте розмір матриці
 та вводити елементи матриці.
та вводити елементи матриці.
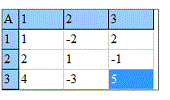 Після обчислень Ви отримаєте елементи матриці доповнень
Після обчислень Ви отримаєте елементи матриці доповнень
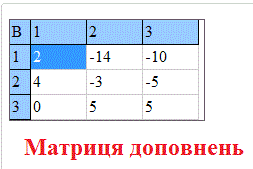 союзної матриці, та оберненої, а також визначник.
союзної матриці, та оберненої, а також визначник. Всі дії розписані детально в окремому вікні
Всі дії розписані детально в окремому вікні і результати обчислень можна зберегти в текстовий файл
і результати обчислень можна зберегти в текстовий файл
 Використовуйте калькулятор для знаходження оберненої матриці та перевірки правильності виконаних Вами обчислень.
Використовуйте калькулятор для знаходження оберненої матриці та перевірки правильності виконаних Вами обчислень.
 Далі задаєте розмір матриці
Далі задаєте розмір матриці та вводити елементи матриці.
та вводити елементи матриці. Після обчислень Ви отримаєте елементи матриці доповнень
Після обчислень Ви отримаєте елементи матриці доповнень союзної матриці, та оберненої, а також визначник.
союзної матриці, та оберненої, а також визначник. Всі дії розписані детально в окремому вікні
Всі дії розписані детально в окремому вікні і результати обчислень можна зберегти в текстовий файл
і результати обчислень можна зберегти в текстовий файл Використовуйте калькулятор для знаходження оберненої матриці та перевірки правильності виконаних Вами обчислень.
Використовуйте калькулятор для знаходження оберненої матриці та перевірки правильності виконаних Вами обчислень.
Приклад 2. Знайти обернену матрицю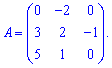 Розв'язання: Обчислюємо визначник матриці розкладом за першим рядком. Це досить зручно оскільки маємо два елементи, які рівні нулю
Розв'язання: Обчислюємо визначник матриці розкладом за першим рядком. Це досить зручно оскільки маємо два елементи, які рівні нулю
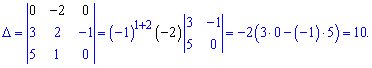
Алгебраїчні доповнення знаходимо скориставшись наведеною вище схемою знаків мінорів
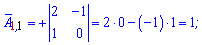
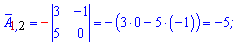
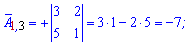
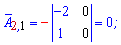
Якщо у визначнику рядок чи стовпець містить елементи =0, то визначник =0.
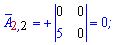
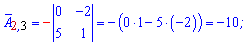
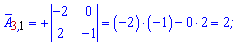
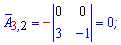
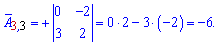
Записуємо матрицю алгебраїчних доповнень
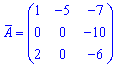
Приєднану матрицю знаходимо транспонуванням знайденої
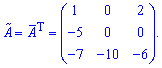
Знаходимо обернену матрицю за відомою формулою
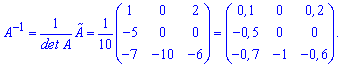
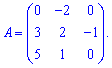 Розв'язання: Обчислюємо визначник матриці розкладом за першим рядком. Це досить зручно оскільки маємо два елементи, які рівні нулю
Розв'язання: Обчислюємо визначник матриці розкладом за першим рядком. Це досить зручно оскільки маємо два елементи, які рівні нулю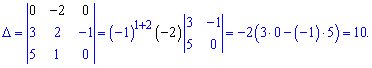
Алгебраїчні доповнення знаходимо скориставшись наведеною вище схемою знаків мінорів
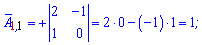
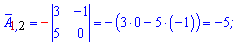
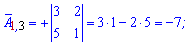
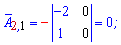
Якщо у визначнику рядок чи стовпець містить елементи =0, то визначник =0.
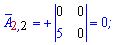
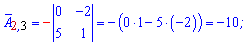
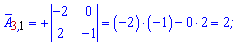
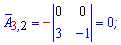
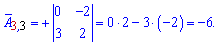
Записуємо матрицю алгебраїчних доповнень
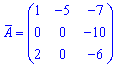
Приєднану матрицю знаходимо транспонуванням знайденої
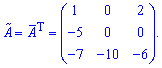
Знаходимо обернену матрицю за відомою формулою
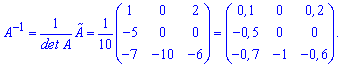
Дякую за інформацію. Ось ще доволі цікавий матеріал по темі: https://www.mathros.net.ua/znaxodzhennya-oberneno%d1%97-matrici-vikoristovuyuchi-koeficiyenti-%d1%97%d1%97-xarakteristichnogo-mnogochlena.html
ВідповістиВидалити