Розв'язування багатьох задач математики, економіки, статистики, механіки, зводиться до розв'язування систем лінійних алгебраїчних рівнянь.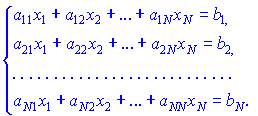 В результаті обчислень отримуємо, що система має один розв'язок, безліч або немає жодного.
В результаті обчислень отримуємо, що система має один розв'язок, безліч або немає жодного.
Давайте вияснимо від чого це залежить?
Розглянемо, для прикладу два лінійних рівняння з двома невідомими:
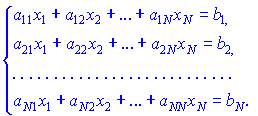 В результаті обчислень отримуємо, що система має один розв'язок, безліч або немає жодного.
В результаті обчислень отримуємо, що система має один розв'язок, безліч або немає жодного.Давайте вияснимо від чого це залежить?
Розглянемо, для прикладу два лінійних рівняння з двома невідомими:
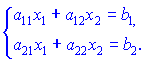
Для розв'язування цих рівнянь ми повинні помножити їх на відповідні множники, при яких виключається одне з невідомих 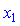 або
або 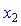 : перше на
: перше на 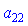 мінус друге на
мінус друге на 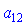 для знаходження
для знаходження 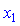 ; друге на
; друге на 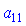 мінус перше на
мінус перше на 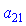 для знаходження
для знаходження 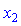
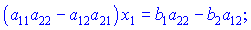
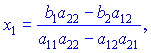
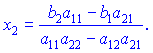 Формули вірні при умові, що знаменник не дорівнює нулю
Формули вірні при умові, що знаменник не дорівнює нулю
Визначником другого порядку називається число, яке дорівнює різниці добутків елементів головної і допоміжної діагоналей, тобто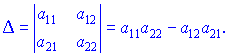 Визначником третього порядку знаходять за правилом трикутників
Визначником третього порядку знаходять за правилом трикутників
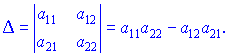 Визначником третього порядку знаходять за правилом трикутників
Визначником третього порядку знаходять за правилом трикутників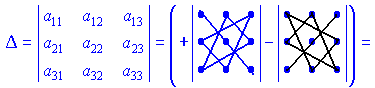
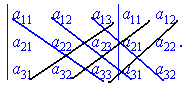
Даний метод обчислення визначника третього порядку називається правилом Саррюса. В процесі обчислень систем лінійних рівнянь встановлено, що визначники рівні сумі доданків, які визначаються як добуток елементів, взятих по одному водночас з кожного рядка і стовпця. Для системи трьох рівнянь в добуток входить три елементи, чотирьох – чотири і т. д. Кількість доданків в визначнику в загальному рівна факторіалу кількості рівнянь. У випадках нульових коефіцієнтів при невідомих знаходження визначника спрощується. Для обчислення визначників старших порядків використовують правила.
ВЛАСТИВОСТІ ВИЗНАЧНИКІВ
1. Величина визначника не зміниться, якщо його рядки замінити стовпчиками, причому кожен рядок замінюють стовпчиком з тим же самим номером (транспонування).
2. Якщо у визначнику поміняти місцями лише два рядки (або два стовпчики), то визначник змінює знак на протилежний, зберігаючи своє абсолютне значення.
3. Якщо визначник має два однакових стовпчики або два однакових рядки, то він рівний нулеві.
4. Якщо визначник містить два пропорційних рядки (стовпчики), то його значення дорівнює нулю. Якщо елементи деякого рядка (стовпчика) дорівнюють нулю, то і сам визначник дорівнює нулю.
5. Якщо всі елементи деякого рядка (стовпчика) помножити на стале число, то значення визначника також помножиться на це число. Звідси слідує, що спільний множник всіх елементів рядка (стовпчика) можна винести за знак визначника.
Як і коли застосовувати основні властивості визначників для спрощення розрахунків Ви знатимете прочитавши наведені в посиланні приклади.
Визначник 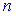 -го порядку, за правилом, рівний сумі добутків елементів довільного рядка або стовпця, на відповідні алгебраїчні доповнення. Уявно викреслимо у визначнику
-го порядку, за правилом, рівний сумі добутків елементів довільного рядка або стовпця, на відповідні алгебраїчні доповнення. Уявно викреслимо у визначнику 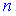 -го порядку
-го порядку 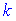 -й рядок і
-й рядок і 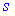 -й стовпець, а з решти елементів утворимо визначник (
-й стовпець, а з решти елементів утворимо визначник (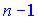 )-го порядку зі збереженням розміщення рядків і стовпців. Отриманий визначник називається мінором визначника і позначається
)-го порядку зі збереженням розміщення рядків і стовпців. Отриманий визначник називається мінором визначника і позначається 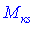
Алгебраїчне доповнення 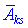 елемента
елемента 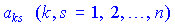 визначника можна подати у вигляді
визначника можна подати у вигляді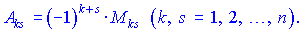
Приклад 1 Знайти визначник 4-го порядку
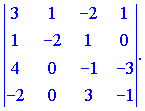
Розв'язок. Розкладемо визначник за елементами другого стовпця
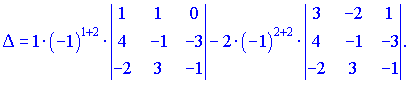
Перший визначник розкладемо за першим рядком
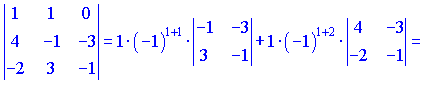
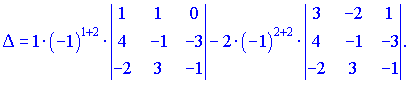
Перший визначник розкладемо за першим рядком
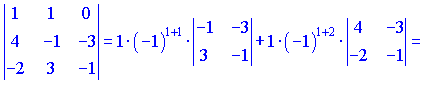
Другий обчислимо за правилом
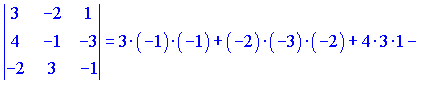
Підставляючи в формулу для визначника, отримаємо
Немає коментарів:
Дописати коментар