Обернена матриця. Приклади обчислення
Знаходження оберненої матриці є важливою складовою в розділі лінійної алгебри. З допомогою таких матриць, якщо вони існують, можна швидко знайти розв'язок системи лінійних рівнянь або обчислити матричне рівняння A*X=B.
Матриця A-1 називається оберненою до матриці A, якщо виконуються наступні рівності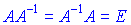 Якщо визначник матриці A відмінний від нуля, то матрицю називають неособливою або невиродженою. Для того, щоб матриця мала обернену необхідно і достатньо, щоб вона була невиродженою.
Якщо визначник матриці A відмінний від нуля, то матрицю називають неособливою або невиродженою. Для того, щоб матриця мала обернену необхідно і достатньо, щоб вона була невиродженою.
Матриця A-1 називається оберненою до матриці A, якщо виконуються наступні рівності
АЛГОРИТМ ЗНАХОДЖЕННЯ ОБЕРНЕНОЇ МАТРИЦІ
Нехай маємо квадратну матрицю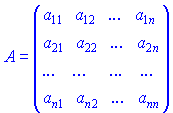 і потрібно знайти обернену до неї. Для цього потрібно виконати наступні дії:
і потрібно знайти обернену до неї. Для цього потрібно виконати наступні дії:
 і потрібно знайти обернену до неї. Для цього потрібно виконати наступні дії:
і потрібно знайти обернену до неї. Для цього потрібно виконати наступні дії:
1. Знайти визначник матриці 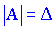 . Якщо він не рівний нулю то виконуємо наступні дії. В іншому випадку дана матриця вироджена і для неї не існує оберненої.
. Якщо він не рівний нулю то виконуємо наступні дії. В іншому випадку дана матриця вироджена і для неї не існує оберненої.
2. Знайти алгебраїчні доповнення елементів матриці A. Вони рівні мінорам, помноженим на (-1)i+j в степені суми рядка і стовпця, для якого шукаємо.
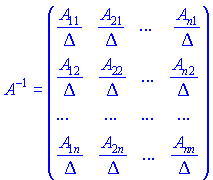
3. Скласти матрицю з алгебраїчних доповнень елементів матриці A та протранспонувати її. Ця матриця називається приєднаною або союзною і позначається "А з хвиькою"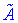 .
.
4. Поділити приєднану матрицю на детермінант 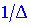 . Отримана матриця буде оберненою та задовільнятиме властивостям, які викладені на початку статті.
. Отримана матриця буде оберненою та задовільнятиме властивостям, які викладені на початку статті.
Розглянемо приклади обчислення оберненої матриці.
Приклад 1. Знайти матрицю, обернену до матриці (Дубовик В.П., Юрик І.І. "Вища математика. Збірник задач")
1) (1.127)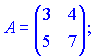
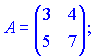
Розв'язок. Обчислюємо визначник матриці
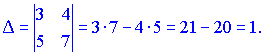
Так як детермінант не рівний нулю (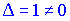 ), то обернена матриця існує. Знаходимо матрицю, складену з алгебраїчних доповнень
), то обернена матриця існує. Знаходимо матрицю, складену з алгебраїчних доповнень
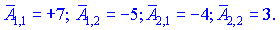
Матриця доповнень набуде вигляду
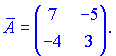
Транспонуємо її і отримуємо приєднану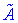
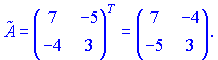
Поділимо матрицю на визначник і отримаємо обернену
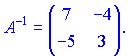
Бачимо, що у випадку, коли визначник рівний одиниці приєднана і обернена матриці співпадають.
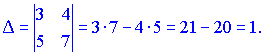
Так як детермінант не рівний нулю (
Матриця доповнень набуде вигляду
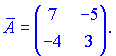
Транспонуємо її і отримуємо приєднану
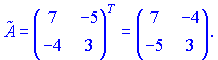
Поділимо матрицю на визначник і отримаємо обернену
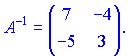
Бачимо, що у випадку, коли визначник рівний одиниці приєднана і обернена матриці співпадають.
2) (1.130)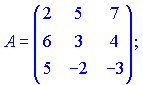
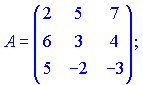
Розв'язок. Рахуємо визначник матриці 3 порядку
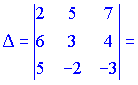
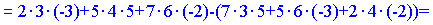
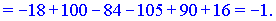
Знаходимо матрицю алгебраїчних доповнень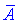 . Для наглядності ми випасали як це робити через мінори (детермінанти) другого порядку
. Для наглядності ми випасали як це робити через мінори (детермінанти) другого порядку
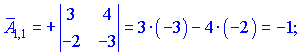
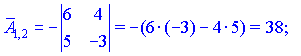
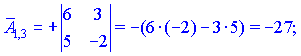
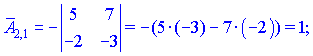
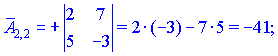
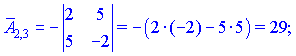
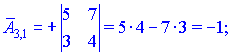
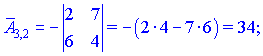
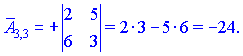
Кінцевий вигляд матриці доповнень наступний
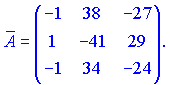
Протранспонувавши її, знайдемо союзну матрицю
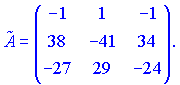
Далі знаходимо обернену матрицю
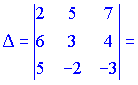
Знаходимо матрицю алгебраїчних доповнень
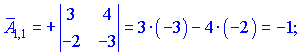
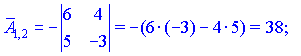
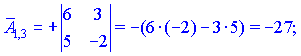
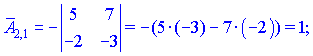
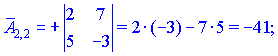
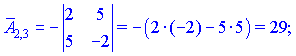
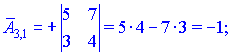
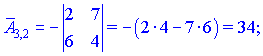
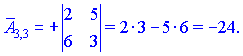
Кінцевий вигляд матриці доповнень наступний
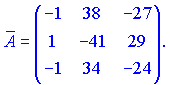
Протранспонувавши її, знайдемо союзну матрицю
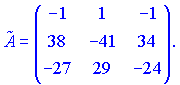
Далі знаходимо обернену матрицю
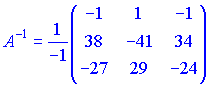
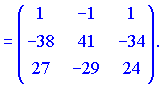
Посідовність дій досить проста, головне тут навчитися знаходити мінори, а вже через них алгебраїчні доповнення.
3) (1.133)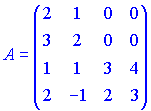
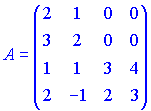
Розв'язок. Обчислимо детермінант матриці 4 порядку. Для цього розкладемо його за першим рядком (містить два нульові елементи). В результаті отримаємо два відмінні від нуля доданки
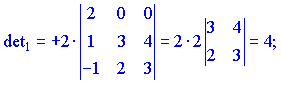
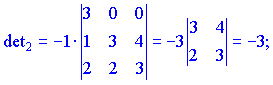
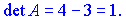
Знаходимо матрицю алгебраїчних доповнень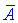 . Розклад визначника проводимо по рядках і стовпцях, в яких найбільше нульових елементів (позначені чорним кольором).
. Розклад визначника проводимо по рядках і стовпцях, в яких найбільше нульових елементів (позначені чорним кольором).
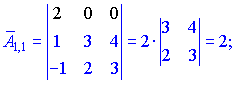
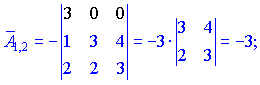
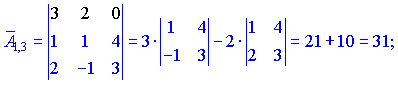
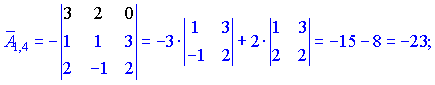
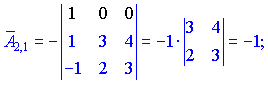
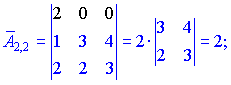
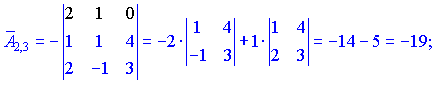
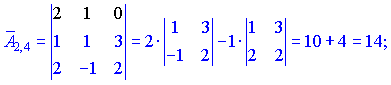
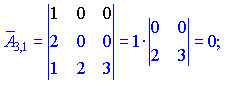
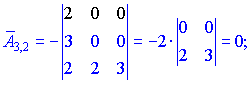
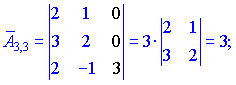
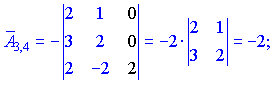
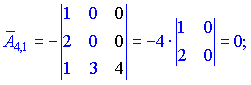
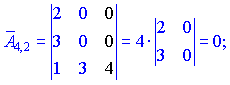
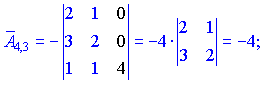
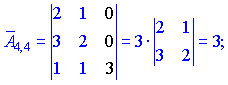
Ми тільки що знайшли 16 мінорів-визначників третього порядку. Знак перед визначником перетворює мінор в алгебраїчне доповнення.
Записуємо результати обчислень в матрицю доповнень
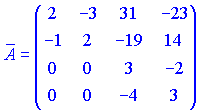
Протранспонувавши її, знаходимо приєднану матрицю
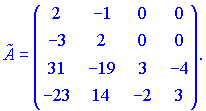
Оскільки визначник головної матриці рівний одиниці, то обернена матриця співпадає з приєднаною. Даний приклад повністю розв'язано.
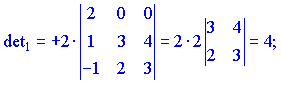
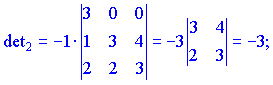
Знаходимо матрицю алгебраїчних доповнень
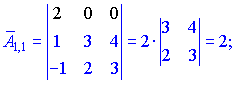
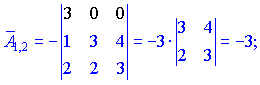
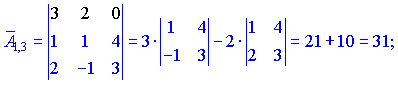
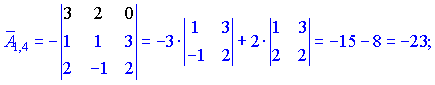
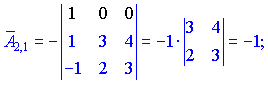
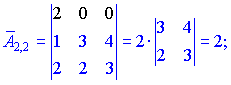
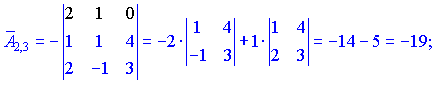
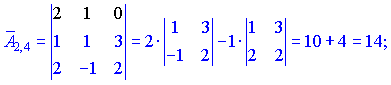
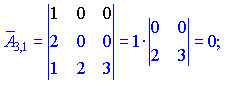
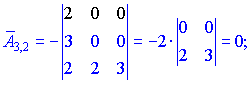
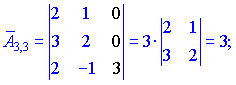
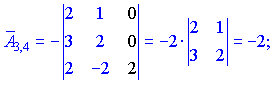
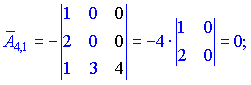
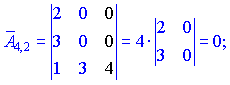
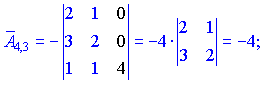
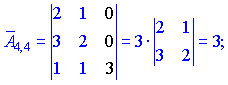
Ми тільки що знайшли 16 мінорів-визначників третього порядку. Знак перед визначником перетворює мінор в алгебраїчне доповнення.
Записуємо результати обчислень в матрицю доповнень
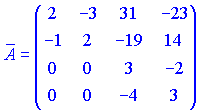
Протранспонувавши її, знаходимо приєднану матрицю
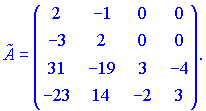
Оскільки визначник головної матриці рівний одиниці, то обернена матриця співпадає з приєднаною. Даний приклад повністю розв'язано.
Немає коментарів:
Дописати коментар