Види матриць. Операції додаванння,віднімання, транспонування, множення
Матрицями називають математичні об'єкти, які мають вигляд таблиць з числовими елементами. Ці елементи обрамляють круглими дужками, а самі матриці позначають великими латинськими літерами.

В складних числових розрахунках можна зустріти трьох вимірні матриці (у вигляді кубиків) та багатовимірні. Однак Ви їх при здобутті вищої освіти зустрічати точно не будете, тому далі мова піде тільки про знайомі для більшості матриці. Горизонталі елементи матриці називають елементами рядків, вертикальні – відповідно елементами стовпців. В позначеннях розмірності матриці першим йде індекс який вказує кількість рядків, другий кількість стовпців. Наприклад, запис 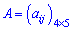 вказує на те, що матриця має 4 рядки і 5 стовпців.
вказує на те, що матриця має 4 рядки і 5 стовпців.
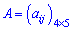 вказує на те, що матриця має 4 рядки і 5 стовпців.
вказує на те, що матриця має 4 рядки і 5 стовпців.
ВИДИ МАТРИЦЬ
В залежності від розмірності та вмісту матриці поділяють на
1) Квадратні 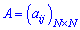 та прямокутні матриці
та прямокутні матриці 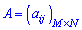 . Наприклад,
. Наприклад,
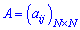 та прямокутні матриці
та прямокутні матриці 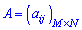 . Наприклад,
. Наприклад,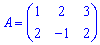 – прямокутна матриця;
– прямокутна матриця;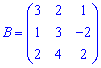 – квадратна матриця.
– квадратна матриця.
2) Одинична матриця – по головній діагоналі одиниці, решта всі елементи рівні нулеві. Позначають великою латинською літерою E.
Для прикладу, матриця
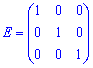 є одиничною матрицею третього порядку.
є одиничною матрицею третього порядку.
3) Діагональна – елементи поза головною діагоналлю нульові, на головній – будь-які. Наприкалад, матриця
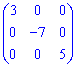
4) Симетрична матриця – елементи такої матриці симетричні відносно головної діагоналі 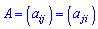 .
.
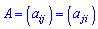 .
.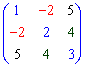
5) Верхня трикутна (нижня трикутна ) матриця – елементи під діагоналлю (над діагоналлю) в таких матрицях нульові. Наприклад,
Верхня трикутна – 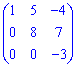
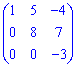
Нижня трикутна 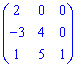
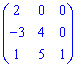
У випадку, коли елементи головної діагональні в трикутній матриці одиничні її називають унітрикутною
ОПЕРАЦІЇ НАД МАТРИЦЯМИ
Основними операціями над матрицями є додавання, віднімання, множення, транспонування. Щоб легше Вам було зрозуміти правила ми наведемо короткі приклади.
Сумою (різницею) двох матриць називають матрицю, елементи якої утворюються попарним додаванням (відніманням) елементів матриць. Для прикладу, додавання двох матриць
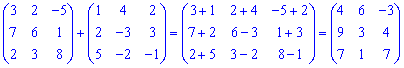
та їх різниця
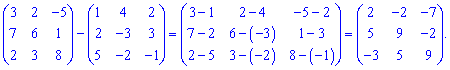
Слід зазначити, що додавати та віднімати можна лише матриці однакових розмірів, тобто кількість рядків першої матриці має дорівнювати кількості рядків другої, те саме стосується і стовпців. Однак кількість рядків і стовпців матриць може не співпадати, тобто сумувати та шукати різниці можна як для квадратних матриць так і для прямокутних.
Транспонуванням матриці називають впорядковану заміну рядків матриці стовпцями і позначають 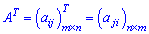 .
.
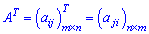 .
.
На практиці транспонування матриці виглядає наступним чином
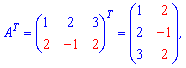
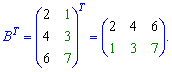
Вибирайте, що Вам візуально зрозуміліше – обидва варіанти дають правильний результат.
Властивості операцій транспонування матриць запишемо в матричному вигляді
1) 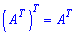
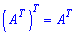
2) 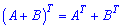
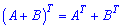
3) 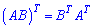
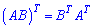
Результатом множення матриці 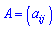 на число
на число  буде матриця
буде матриця  , елементи якої збільшені в
, елементи якої збільшені в  разів порівняно з
разів порівняно з 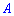 , тобто
, тобто 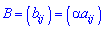 .
.
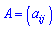 на число
на число  буде матриця
буде матриця  , елементи якої збільшені в
, елементи якої збільшені в  разів порівняно з
разів порівняно з 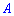 , тобто
, тобто 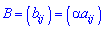 .
.
Множення (добуток) двох матриць 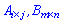 знаходять за правилом, яке можна застосувати лише до матриць в яких кількості стовпців першої та рядків другої матриці співпадають
знаходять за правилом, яке можна застосувати лише до матриць в яких кількості стовпців першої та рядків другої матриці співпадають 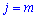 . В результаті отримують матрицю
. В результаті отримують матрицю 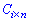 , розмірності кількості рядків першої на стовпців другої з елементами
, розмірності кількості рядків першої на стовпців другої з елементами 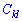 , які рівні сумі попарних добутків елементів
, які рівні сумі попарних добутків елементів 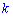 -го рядка першої матриці, на елемент
-го рядка першої матриці, на елемент 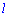 -го стовпця другої матриці.
-го стовпця другої матриці.
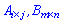 знаходять за правилом, яке можна застосувати лише до матриць в яких кількості стовпців першої та рядків другої матриці співпадають
знаходять за правилом, яке можна застосувати лише до матриць в яких кількості стовпців першої та рядків другої матриці співпадають 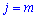 . В результаті отримують матрицю
. В результаті отримують матрицю 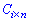 , розмірності кількості рядків першої на стовпців другої з елементами
, розмірності кількості рядків першої на стовпців другої з елементами 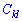 , які рівні сумі попарних добутків елементів
, які рівні сумі попарних добутків елементів 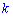 -го рядка першої матриці, на елемент
-го рядка першої матриці, на елемент 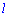 -го стовпця другої матриці.
-го стовпця другої матриці.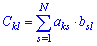
На перший погляд складне і запутане правило досить легко пояснити на практиці. Нехай маємо дві матриці
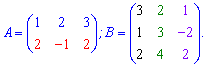
Елементи рядків першої і стовпців другої позначимо в різні кольори для того, щоб Вам наочніше продемонструвати правило множення матриць. Умова рівності кількості стовпців першої матриці = кількості рядків другої виконується (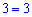 ).
).
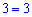 ).
).
Виконуємо обчислення елементів добутку матриць
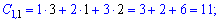
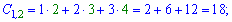
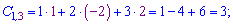
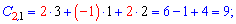
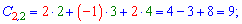
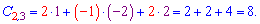
Записуючи матрицю в табличному вигляді
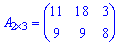
легко переконатися, що утворена матриця має розмірність 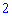 – кількості рядків першої матриці на
– кількості рядків першої матриці на 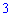 – кількість стовпців другої (про що і було сказано в правилі). За тими ж правилами знаходять добутки квадратних і прямокутних матриць великих розмірів, кількість обчислень при цьому зростає.
– кількість стовпців другої (про що і було сказано в правилі). За тими ж правилами знаходять добутки квадратних і прямокутних матриць великих розмірів, кількість обчислень при цьому зростає.
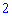 – кількості рядків першої матриці на
– кількості рядків першої матриці на 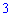 – кількість стовпців другої (про що і було сказано в правилі). За тими ж правилами знаходять добутки квадратних і прямокутних матриць великих розмірів, кількість обчислень при цьому зростає.
– кількість стовпців другої (про що і було сказано в правилі). За тими ж правилами знаходять добутки квадратних і прямокутних матриць великих розмірів, кількість обчислень при цьому зростає.
Додавання та множення матриць можна охарактеризувати властивостями:
1) 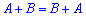 – комутативність
– комутативність
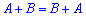 – комутативність
– комутативність
2) 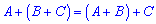 – асоціативність
– асоціативність
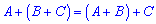 – асоціативність
– асоціативність
3) 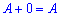
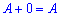
Для будь якої ненульової матриці існує протилежна матриця 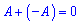
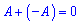
4) Константу можна виносити за правилом 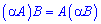
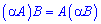
5) Асоціативність множення
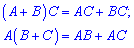
6) 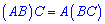
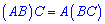
Множення матриць не є комутативною операцією, тобто
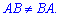
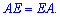
Комутативність має місце лише у випадку коли матриці – квадратні і одна з них є оберненою до іншої, але про це мова піде в наступних статтях. Зараз постарайтеся розібратися з наведеним матеріалом, він стане Вам в нагоді при вивченні складніших операцій з матрицями.
Немає коментарів:
Дописати коментар