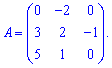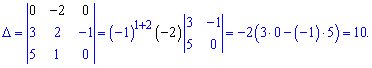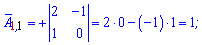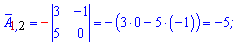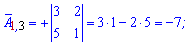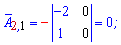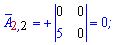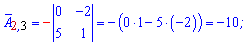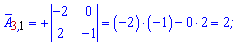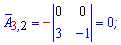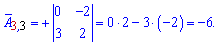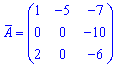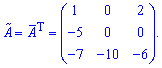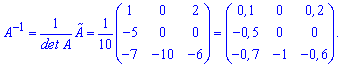Калькулятор для матриць

https://www.kontrolnaya-rabota.ru/s/matrix/#reversion

рішення матриць

Отже, сервіси за рішенням матриць онлайн:

• зворотна матриця
• визначник матриці
• множення матриць
• транспонування матриці
• Ранг матриці
• Власні значення і власні вектори
• Перетворення матриці до трикутного вигляду
• Зведення матриці в ступінь
• Комплексно-сполучена матриця
• розклад матриці
• сума матриць
• Множення матриці на число
• віднімання матриць

Сервіс роботи з матрицями дозволяє виконати елементарні перетворення матриць. 
Якщо у Вас стоїть завдання виконати більш складне перетворення, то цим сервісом варто користуватися як конструктором.

Приклад . Дано матриці A і B , треба знайти C = A ^-1 * B + B ^T ,

1. Вам варто спочатку знайти зворотну матрицю A1 = A ^-1 , скориставшись сервісом по знаходженню оберненої матриці ;
2. Далі, після того, як знайшли матрицю A1 виконаємо множення матриць A2 = A1 * B , скориставшись сервісом по множенню матриць ;
3. Виконаємо транспонування матриці A3 = B ^T ( сервіс по знаходженню транспонованою матриці );
4. І останнє - знайдемо суму матриць С = A2 + A3 ( сервіс по обчисленню суми матриць ) - і отримуємо відповідь з самим докладним рішенням !;

твір матриць

Це он-лайн сервіс в два кроки :

• Ввести перший співмножник матрицю A
• Ввести другий співмножник матрицю або вектор-стовпець B

Перейти: Онлайн сервіс "Множення матриць" →

Множення матриці на вектор

Множення матриці на вектор можна знайти, скориставшись сервісом Множення матриць
(Першим співмножником буде дана матриця, другим співмножником буде стовпець, що складається з елементів даного вектора)

зворотна матриця

Це он-лайн сервіс в два кроки :

• Введіть матрицю A , для якої потрібно знайти зворотну матрицю
• Отримайте відповідь з докладним рішенням по знаходженню оберненої матриці

Перейти: Онлайн сервіс "Зворотній матриця" →

визначник матриці

Це он-лайн сервіс в один крок :

• Введіть матрицю A , для якої потрібно знайти визначник матриці

Перейти: Онлайн сервіс "Визначник матриці" →

транспонування матриці

Тут Ви зможете відстежити алгоритм транспонування матриці і навчитися самому вирішувати подібні завдання.

Це он-лайн сервіс в один крок :

• Введіть матрицю A , яку треба транспонувати

Перейти: Онлайн сервіс "Транспонування матриці" →

Ранг матриці

Це он-лайн сервіс в один крок :

• Введіть матрицю A , для якої потрібно виконати знаходження рангу

Перейти: Онлайн сервіс "Ранг матриці" →

Власні значення матриці і власні вектора матриці

Це он-лайн сервіс в один крок :

• Введіть матрицю A , для якої потрібно знайти власні вектора і власні значення (власні числа)

Перейти: Онлайн сервіс "Власні вектора і власні значення матриці" →

Зведення матриці в ступінь

Це он-лайн сервіс в два кроки :

• Введіть матрицю A , яку будете підносити до степеня
• Ввести ціле число q - ступінь

Перейти: Онлайн сервіс "Зведення матриці в ступінь" →

Зведення матриці в негативну ступінь

Щоб подивитися результат зведення матриці A в негативну ступінь q - потрібно скористатися цим же сервісом "Зведення матриці в ступінь", тільки q буде негативним цілим числом

Комплексно-зв'язані матриці

Цей калькулятор знаходить ермітовим-сполучену матрицю і комплексно-сполучену Дирака 
Комплексно-сполучена матриця онлайн

розклад матриці

Дані калькулятори дають QR-розкладання, LU-розкладання, розкладання Холецкого матриць онлайн

• QR-розкладання матриці
• LU-розкладання матриці
• Розкладання матриці Холецкого

Приведення матриці до трикутного вигляду

Цей калькулятор як результат повертає матрицю, наведену до верхнетреугольному увазі і ніжнетреугольному увазі 
Перейти до Трикутний вид матриці

сума матриць

Це он-лайн сервіс складання в два кроки :

• Ввести перший доданок матрицю A
• Ввести другий доданок матрицю B

Перейти: Онлайн сервіс "Сума матриць" →

Множення матриці на число

Це он-лайн сервіс множення в два кроки :

• Ввести перший співмножник матрицю A
• Ввести другий співмножник число q

Перейти: Онлайн сервіс "Множення матриці на число" →

віднімання матриць

Це он-лайн сервіс в три кроки :

• Ввести першу матрицю, яку віднімають A
• Ввести другу матрицю, з якої віднімають B
• Після ви отримаєте докладний рішення з результатом віднімання матриць

Перейти: Онлайн сервіс "Віднімання матриць" →

транспонування матриці

Ранг матриці та способи його обчислення

Рангом матриці називається найвищий порядок відмінних від нуля мінорів. Його позначають через r або rang(A).

ВЛАСТИВОСТІ РАНГУ МАТРИЦІ

1. Ранг матриці рівний нулю лише для нульової матриці. В інших випадках ранг матриці рівний деякому додатному числу.
2. Ранг прямокутної матриці не перевищує меншого із двох чисел m і n, тобто 
3. Для квадратної матриці n-го порядку r=n тільки тоді, коли матриця невироджена.
4. У випадку квадратної матриці, якщо r<n то визначник матриці дорівнює нулю.

При знаходженні рангу матриці, як правило, треба обчислювати велику кількість визначників. Щоб полегшити задачу студентам давно-давним знайдені елементарні перетворення за допомогою яких можна, злегка помінявши вигляд матриці, без обчислення визначників порахувати ранг.

ЕЛЕМЕНТАРНІ ПЕРЕТВОРЕННЯ

1. Транспонування, тобто заміна кожного рядка стовпчиком з тим ж номером і навпаки.
2. Перестановка двох рядків або двох стовпчиків.
3. Множення всіх елементів рядка або стовпчика на будь-яке число не рівне нулю.
4. Додавання до всіх елементів рядка або стовпчика відповідних елементів паралельного ряду, помноженого на одне і те ж число.

Матриці, одержані одна з другої елементарними перетвореннями, називаються еквівалентними. Еквівалентні матриці не рівні одна одній, але при елементарних перетвореннях матриці її ранг не змінюється. Якщо матриці A і Bеквівалентні, то це записують так: 
Розглянемо два основних методи знаходження рангу матриці.

Перший метод – метод окантування – полягає у наступному:

Якщо всі мінори І-го порядку, тобто елементи матриці, рівні нулю, то r=0.
Якщо хоч один із мінорів 1-го порядку не дорівнює нулю, а всі мінори 2-го порядку дорівнюють нулю, то r=1.
Якщо мінор 2-го порядку відмінний від нуля, то досліджуємо мінори 3-го порядку. Таким способом знаходять мінор k-го порядку і перевіряють, чи не дорівнюють нулю мінори k+1-го порядку.
Якщо всі мінори k+1-го порядку дорівнюють нулю, то ранг матриці A(aij)m,n дорівнює числу k. Такі мінори k+1-го порядку, як правило, знаходять шляхом "окантування " мінора k-го порядку.

Другий метод визначення рангу матриці полягає в застосуванні елементарних перетворень матриці при зведенні її до діагонального вигляду. Ранг такої матриці дорівнює кількості відмінних від нуля діагональних елементів.
Розглянемо приклади застосування кожного методу.

Приклад 1. Знайти ранг матриці A методом окантування.

Розв'язок. Матриця A(aij)4,5 містить ненульові елементи мінори 1-го порядку, отже її ранг може бути рівний одиниці. Згідно правила ранг матриці не перевищує чотирьом r<=4. Мінор 2-го порядку

рівний нулю, але наступний мінор

відмінний від нуля. Окантовуючи мінор другого порядку перевіримо третій: для цього розкладемо його по третьому стовпчику

Розглянемо мінор четвертого порядку, що окантовує даний

Він рівний нулю, оскільки останній рядок нульовий. Лишається обчислити ще один мінор


Шуканий ранг матриці рівний чотирьом (r=4). На прикладі можна бачити, що вибір окантування не завжди можна вдало вибрати і потрібно числити велику кількість мінорів.

Приклад 2. Знайти ранг матриці A.

Розв'язок. 1. Переставимо четвертий стовпець на перше місце, а всі решта змістимо вправо.
2. Занулимо всі елементи в першому рядку після 1. Для цього до 2,3,4,5 стовпців додамо перший помножений на -3; -2; 2; -5 відповідно.
3. Третій стовпець поділимо на 6. До четвертого і п'ятого стовпців додамо третій, помножений на -1;-3.
4. До п'ятого стовпця додамо четвертий, помножений на 2.
5. Переставимо третій і четвертий стовпці на друге і третє місця, а другий стовпець на місце четвертого.



В вихідній матриці викреслемо останній стовпець з нульовими елементами

Ранг еквівалентної матриці рівний чотирьом, а отже і rang(A)=4. Можна заміти, що матриці в першому і другому прикладах еквівалентні між собою (мають однакові ранги). Таим методом обчислють ранги набагато біьших за розміром матриць, є алгоритми, які дозволяють автоматизувати перевірку рангу матриць і створити корисні для використання калькуятори.

Обернена матриця 3*3.

Як знайти обернену матрицю детально описано в попередніх уроках. Нагадаю лише послідовність обчислень:

• знаходимо визначник головної матриці;
• далі через мінори обчислюємо алгебраїчні доповнення до матриці;
• останнім кроком потрібно протранспонувати матрицю алгебраїчних доповнень (знайти союзну) та поділити на визначник.
• Результатом обчислень і буде обернена матриця.

Нижче наведені приклади покрокового обчислення матриці 3х3. Інструкція дуже добре проілюстрована, тому Вам все стане зрозуміло з першого перегляду.

Приклад 1. Знайти обернену матрицю

Розв'язання: Обчислюємо визначник матриці 3*3 за правилом трикутників

Визначник відмінний від нуля, отже матриця А не вироджена і існує обернена до неї.
Алгебраїчні доповнення рівні мінорам помноженим на (-1) в степені суми рядка і стовпця елемента матриці.
Для простоти можете використовувати наведену нижче схему знаків мінорів
Мінори рівні визначникам на 1 меншого порядку ніж матриця, які утворюються викреслюванням рядка та стовпця на перетині якого знаходиться елемент. Більш зрозуміло стане з наступних прикладів обчислень алгебраїчних доповнень









Із знайдених значень формуємо матрицю алгебраїчних доповнень

Транспонуємо її щоб отримати приєднану (союзну) матрицю

На цьому кроці будьте уважними – можна виконати правильно наведені вище обчислення і через невміння транспонувати отримати невірний результат.
Ділимо на визначник і отримуємо обернену матрицю

Знайти обернену мартицю Вам допоможе калькулятор оберненої матриці YukhymCalc. Для цього заходите в меню калькулятора і вибираєте обчислення обернених матриць
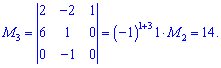
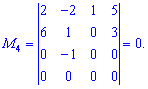
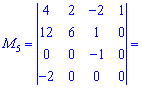
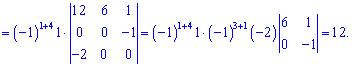
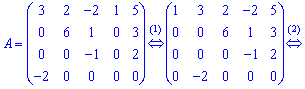
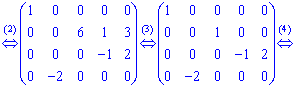
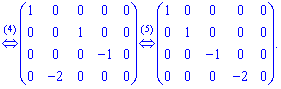
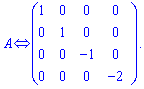
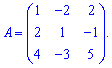
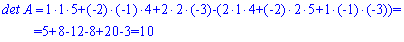
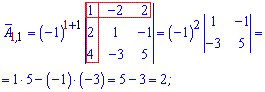
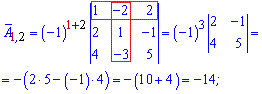
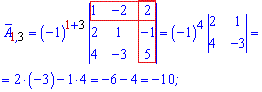
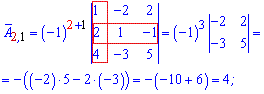
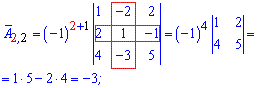
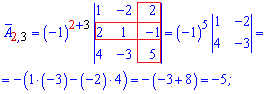
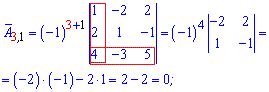
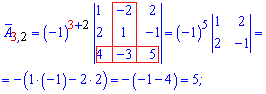
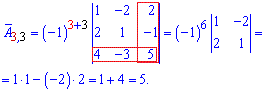
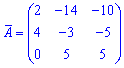
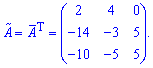
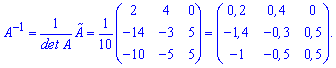
Далі задаєте розмір матриці
та вводити елементи матриці.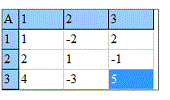
Після обчислень Ви отримаєте елементи матриці доповнень
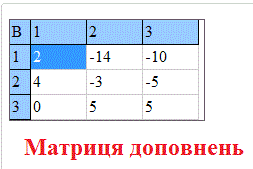союзної матриці, та оберненої, а також визначник.Всі дії розписані детально в окремому вікніі результати обчислень можна зберегти в текстовий файл
Використовуйте калькулятор для знаходження оберненої матриці та перевірки правильності виконаних Вами обчислень.

Приклад 2. Знайти обернену матрицюРозв'язання: Обчислюємо визначник матриці розкладом за першим рядком. Це досить зручно оскільки маємо два елементи, які рівні нулю

Алгебраїчні доповнення знаходимо скориставшись наведеною вище схемою знаків мінорів




Якщо у визначнику рядок чи стовпець містить елементи =0, то визначник =0.





Записуємо матрицю алгебраїчних доповнень

Приєднану матрицю знаходимо транспонуванням знайденої

Знаходимо обернену матрицю за відомою формулою